π y e en el triángulo de Pascal
Lo notable de esta expresión es que la sucesión de los coeficientes que acompañan a las potencias pares de π, junto con dichas potencias — si ignoramos los signos negativos — son los mismos que en los polinomios de Fibonacci (sustituyendo π por x), que pueden encontrarse en diagonales del triángulo de Pascal.
Si tomamos en cuenta los signos negativos, se pueden encontrar los coeficientes de los numeradores al extender el patrón del triángulo de Pascal más allá de la fila 0, en el triángulo de Pascal rotado:
Al cortar la expresión en puntos finitos y resolver los polinomios resultantes se obtienen aproximaciones de π como la siguiente:
≈ 3.1436
Claramente, el problema de aproximaciones como esta es que son muy lentas en cuanto a acercarse al valor de π, y rápidamente se vuelve extremadamente complicado calcularlas. La expresión de la imagen, por ejemplo, es una solución del polinomio truncado en el 5° término de la serie infinita del inicio del post.
La identidad se obtiene al combinar mi fórmula que relaciona a e con los polinomios de Fibonacci (al respecto, véase este post), con la identidad de Euler, conocida como la identidad más bella de todas las matemáticas.
Además, usando el hecho notable de que 1 + 1/3! + 1/5! + 1/7! + 1/9! +... es igual al seno hiperbólico de 1, se obtiene una bella identidad que involucra a π , a e y a los polinomios de Fibonacci:
La demostración directa de la identidad del inicio es bastante sencilla:
De aquí se sigue que:
Así tenemos otra manera (no trivial) de calcular el número e usando el triángulo de Pascal, siendo la única otra manera conocida previamente la de Harlan J. Brothers:
También se deducen las siguientes (infinitas) identidades:
En esta otra identidad, al sustituir π con x, los polinomios resultantes en los numeradores son polinomios de Chebyshev de segundo tipo en posiciones impares.
Al simplificar la expresión obtenemos esta identidad:
Los polinomios de Chebyshev de segundo tipo en posiciones pares guardan esta relación con π:
Una cuestión que surge aquí es la de si existe una secuencia de números en los denominadores que relacione a π con el triángulo de Pascal (1, 3) [y en general triángulos de Pascal tipo (1, n), con n > 2] de manera similar. Por ejemplo si hay una sucesión de números que verifique esta identidad:
Lo más cercano a ello que he encontrado es la siguiente identidad:
La diferencia es que en el triángulo de Pascal (1, 3) se coloca un 0 en la cúspide del triángulo, y un 3 a la derecha de este, lo cual cambia los valores de las entradas y conduce a la identidad.
La identidad análoga para el triángulo de Pascal (1, 4) es:
Reconociendo que 1 + 3/3! + 5/5! + 7/7! + ... = 1 + 1/2! + 1/4! + 1/6! + ... = cosh(1), obtenemos esta identidad:
Y si multiplicamos ambos lados por π en la identidad trasanterior, obtenemos la relación de este último con los polinomios de Chebyshev de primer tipo en posiciones impares:
Esta identidad se puede expresar con una notación más simple:
Y esta identidad relacionan a e y π con polinomios relacionados con los números de Jacobsthal en posiciones pares:
Volviendo al inicio del post, una pregunta interesante es: ¿Qué suma obtenemos si sumamos los términos que corresponden a los polinomios de Fibonacci con índice par? La respuesta es muy interesante:
Nótese que la sucesión 2, 4, 12, 40, 140, ... es la sucesión de los números que son el doble que los coeficientes binomiales centrales:
Si este es de hecho el patrón, ¿quiere decir que el patrón de los coeficientes de π^2 son estos? :
El patrón en general parece ser por ende este:
Y así sucesivamente.
La identidad es esta:
Cada sumando del lado derecho de esta identidad también guarda relación con la función de Bessel de primer tipo y con funciones hipergeométricas. Por ejemplo:
He aquí otra cosa interesante: si en la imagen trasanterior sumamos las entradas en la diagonal, la sucesión de números resultante es la circunvolución de los coeficientes binomiales centrales y la sucesión de Fine. Esta circunvolución tiene una interesante conexión con los números primos dada por Gauss:
Las congruencias de Gauss a(n · p^k) ≡ a(n^p^(k-1)) mod p^k se cumplen para primos p >= 3 y enteros positivos n y k. - Peter Bala, 7 de enero de 2022
Como consecuencia de la relación de la circunvolución con las sucesiones de coeficientes binomiales que se puede observar en la imagen, obtenemos estas identidades combinatorias:
Además:
1 = 1
3 = 3
10 + 1 = 11
35 + 5 = 40
126 + 21 + 1 = 148
462 + 84 + 7 = 553
etc.
(OEIS A014301).
Y curiosamente:
1 = 4 - 3
7 = 4^2 - 3^2
36 + 1 = 4^3 - 3^3
165 + 9 + 1 = 4^4 - 3^4
715 + 55 + 10 + 1 = 4^5 - 3^5
etc.
Un par de conjeturas:
A) Si a(0) = 0, a(1) = 1, y ∀n ∈ ℕ: a(n) = k · a(n - 1) + a(n - 2), con k impar, entonces:
B) Si a(0) = 0, a(1) = 1, y ∀n ∈ ℕ: a(n) = k · a(n - 1) + a(n - 2), con k par, entonces:
Es decir, para n natural:
En general, es posible encontrar identidades para todos los triángulos del siguiente tipo:
0 x
1 x x
1 x + 1 2x
1 x + 2 3x + 1
etc.
Al considerar las diagonales irregulares del triángulo se obtienen relaciones con (e - 1/e)/2, de la forma x · senh(1).
Si tomamos x = 1 obtenemos:
Donde al sumar el valor absoluto de los coeficientes se obtiene uno menos que el doble de un número de Fibonacci con índice impar.
La identidad general es:
Y podemos generalizarla más aún:
Demostrar esta identidad es sorprendentemente fácil:






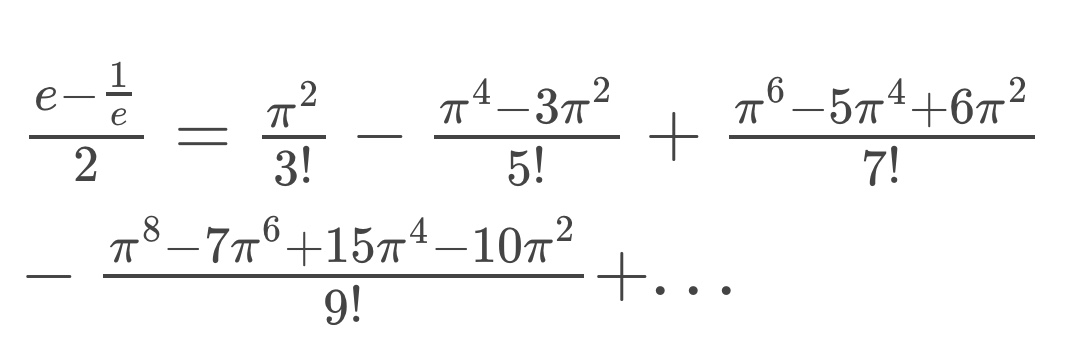


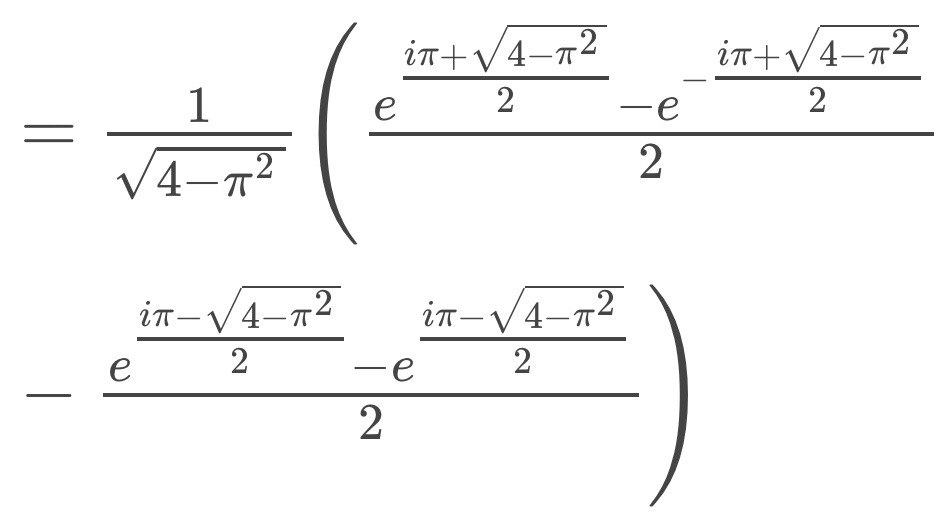












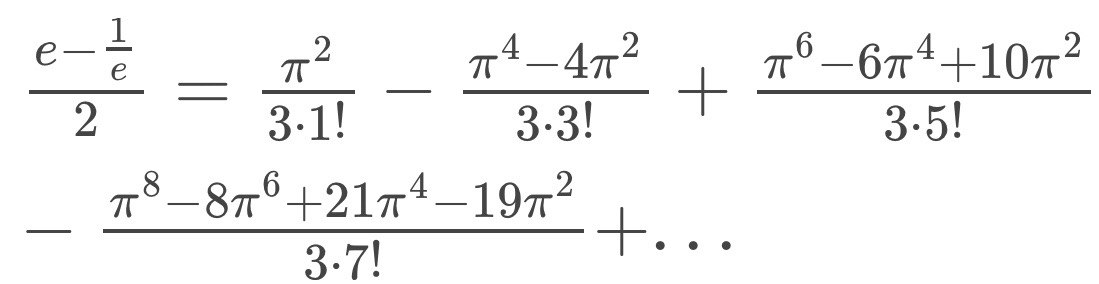





.png)








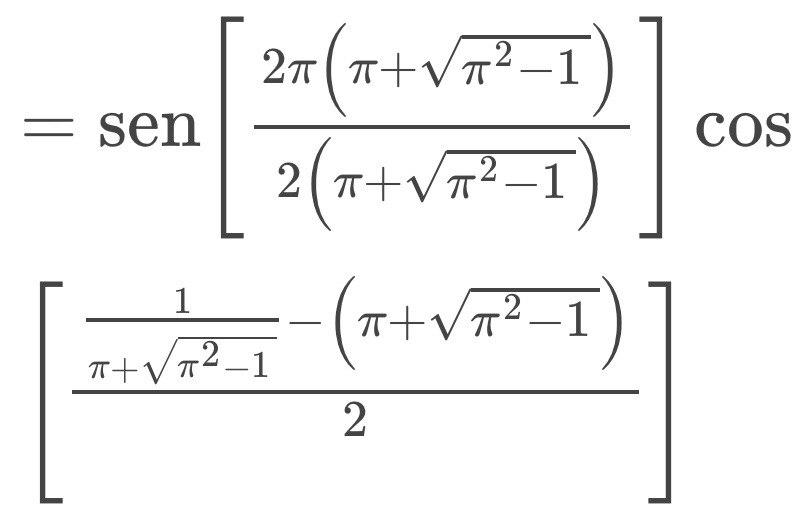





_edit_256611971264489.png)
_edit_257690231279429.png)
_edit_258570271646482.png)








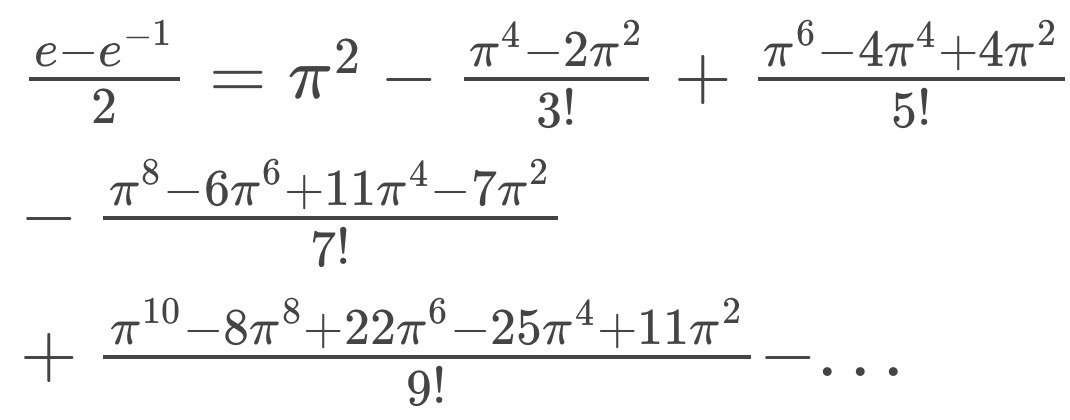








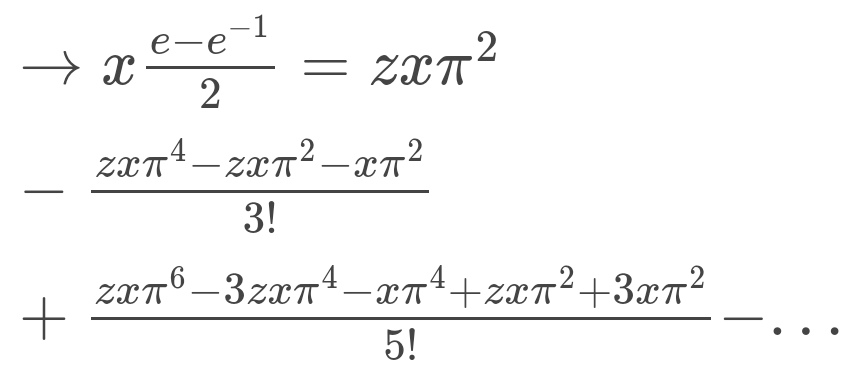




Comentarios
Publicar un comentario