Polinomios de Fibonacci generalizados y la función exponencial

 Defínase la siguiente sucesión de polinomios:


u_ (0) (x, y) = 0

u_ (1) (x, y) = 1

u_(n + 2) (x, y) = x * u_(n+1) (x, y) + y * u_(n) (x, y)


Entonces, se cumple que:



= senh(√y) /√y

Con el siguiente corolario:




La identidad análoga para el seno es:




Lo cual implica que:



Donde senc es el seno cardinal.


Además:




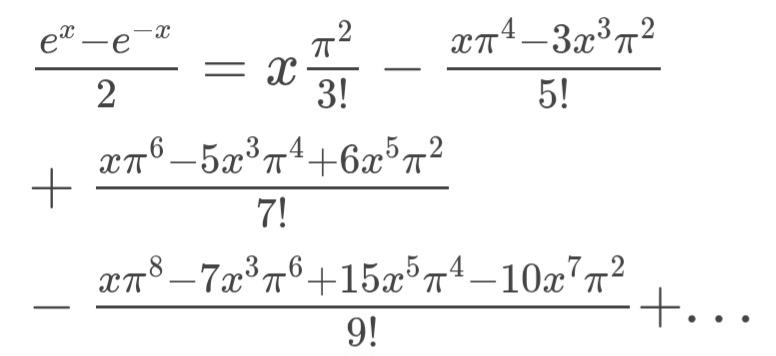
Comentarios

Publicar un comentario

Entradas más populares de este blog

π y e en el triángulo de Pascal

Imagen
Lo notable de esta expresión es que la sucesión de los coeficientes que acompañan a las potencias pares de π, junto con dichas potencias — si ignoramos los signos negativos — son los mismos que en los  polinomios de Fibonacci (sustituyendo π por x ), que pueden encontrarse en diagonales del triángulo de Pascal.  Si tomamos en cuenta los signos negativos, se pueden encontrar los coeficientes de los numeradores al extender el patrón del triángulo de Pascal más allá de la fila 0, en el triángulo de Pascal rotado: Al cortar la expresión en puntos finitos y resolver los polinomios resultantes se obtienen aproximaciones de π como la siguiente: ≈ 3.1436 Claramente, el problema de aproximaciones como esta es que son muy lentas en cuanto a acercarse al valor de π , y rápidamente se vuelve extremadamente complicado calcularlas. La expresión de la imagen, por ejemplo, es una solución del polinomio truncado en el 5° término de la serie infinita del inicio del post. La identidad se ob...
Leer más

La colcha de la señora Perkins

Imagen
  En la imagen las disecciones del cuadrado son coprimas: “El problema es dividir un cuadrado n X n en cuadrados enteros más pequeños, el MCD de cuyos lados es 1, utilizando el menor número de cuadrados posible”. Encontrar la cantidad de cuadrados requeridos para teselar un cuadrado n × n de esta forma sigue siendo un problema abierto.  Conjetura: Se pueden encontrar disecciones tales que  sucesión formada por las sumas de las longitudes de los lados de los cuadrados pequeños de cada cuadrado grande forma una progresión aritmética: siempre se pueden encontrar disecciones mínimas tales que la suma de las longitudes de los lados de cada cuadrado son 3 unidades más que la suma de las longitudes de los lados del cuadrado (n - 1) × (n - 1). En otras palabras, mi conjetura es: siempre es posible, para un cuadrado n × n, encontrar una disección mínima tal que la suma de las longitudes de los lados de los cuadrados resultantes es 3n - 2. Sin embargo, y como me señaló Ed Pegg Jr.,...
Leer más

e y los polinomios de Fibonacci

Imagen
Donde [ φ ^ k ] significa: ( φ ^ k ) redondeado al entero más cercano. Demostración: Esta identidad es el caso x = 1 de esta otra más general: Esto se puede demostrar usando la fórmula de Euler-Binet : Si x es un entero positivo, se obtienen relaciones entre e y otras secuencias de Lucas en los numeradores de las fracciones que están en el numerador de la fracción grande. Por ejemplo, si x = 2 se obtiene la antiguamente llamada “Sucesión de Pibonacci” (3, 1, 4, 5, 9, 14, 23, 37, ...) Por su parte — cuando x = 2 — en los numeradores que están en el denominador de la fracción grande se obtiene la sucesión A013655 (3, 2, 5, 7, 12, 19,...) con los signos alternados, que es además la extensión de la sucesión de Pibonacci hacia la izquierda (..., -19 , 12 , -7 , 5 , -2 , 3 , 1, 4, 5, 9, ...) Esto también aplica para las demás secuencias resultantes al sustituir x por un entero positivo. Si x es una fracción 1/n , y n es un entero positivo, se obtiene en los numeradores de las fraccio...
Leer más